

A user can provide analytical Jacobian matrix for better performance or use built-in parallel function provided by the solver to estimate numerical Jacobian.Can resolve DAE systems of 10 8 equations and even more (depending on the Jacobian matrix sparsity and machine's RAM).Finally, depending on the convergence rate of the Newton method, variability of the solution and user-defined accuracy, the DAE solver may adjust the time step and initiate a new iteration in time. The sparse solver performs 3 steps: reordering and symbolic factorization of Jacobian matrix, then numerical factorization, and then back substitution + iterative refinement.
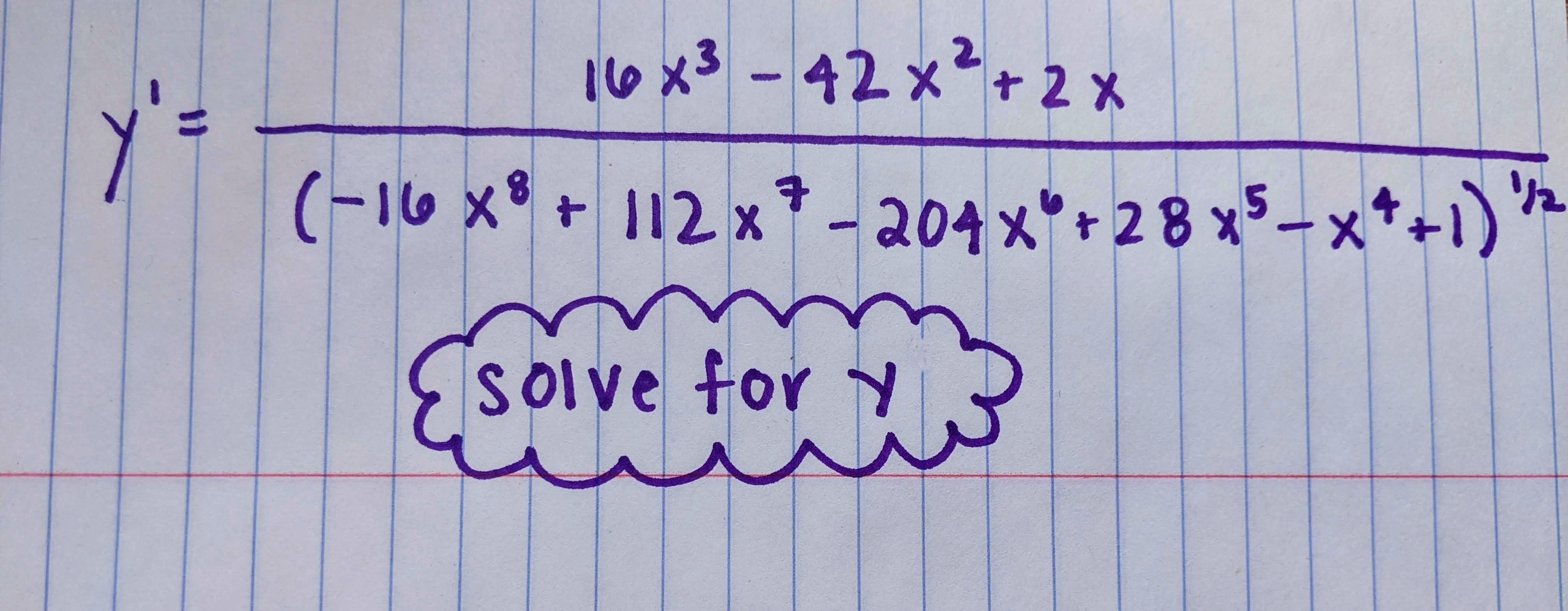
Each Newton iteration a system of linear algebraic equations is solved using Parallel Direct Sparse Solver ( Intel MKL PARDISO). How does it workīDF time stepper reduces the original DAE system to a system of nonlinear equations that is solved using iterative Newton root-finding algorithm. Where Mass matrix M can be singular, and the RHS f( x) is a nonlinear function of a real vector x and time t.įor the numerical integration the solver uses implicit BDF (Backward Differentiation Formula) method of orders 1-6 (can be defined by a user) with adaptive time stepping. The system may contain both differential and algebraic equations and can be written in the following matrix-vector form: What is dae-cppĪ cross-platform, parallel C++ library for solving user-defined, stiff systems of DAEs (an initial value problem).

A simple but powerful C++ solver for Differential Algebraic Equation (DAE) systems.


 0 kommentar(er)
0 kommentar(er)
